The best paper award for UAI 2014 was given to “Firefly Monte Carlo: Exact MCMC with Subsets of Data” by Dougal Maclaurin and Ryan P. Adams. Paraphrasing the title of the famous song (10,000 fireflies) we are hosting a mini interview from Dougal:

NV: Our readers are not experts in Bayesian Inference. Can you describe the Steps of FireFly MCMC in simple and practical steps. Give us an example.

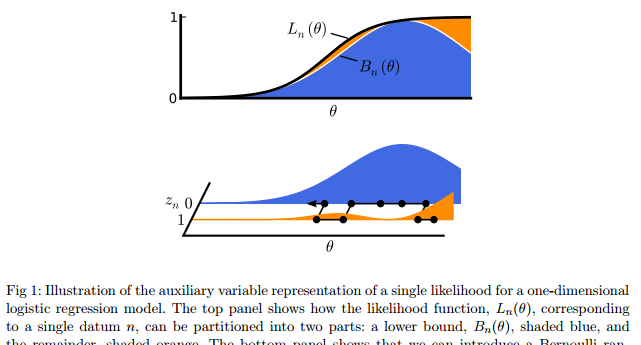
DM: The goal of Markov Chain Monte Carlo (MCMC) is to take a random walk through parameter space in such a way that you fairly sample your distribution of interest. This normally requires evaluating the probability density function at each step. In the case of posterior inference with iid data, the pdf is the product of a likelihood term for each data point and a prior. With lots of data, evaluating each likelihood can take a long time, which is one of the reasons that MCMC has a reputation for being slow. The idea behind Firefly Monte Carlo is to split each likelihood term into two components – a simple component, like a Gaussian, and whatever is left over, which may be complicated. You then introduce a auxiliary variable for each data point which can be in one of two states – let’s call them ‘bright’ and ‘dark’. When the auxiliary variables are bright, you evaluate the complicated component of the likelihood, and when the auxiliary variables are dark, you evaluate the simple part, which is much easier because you can do all the work ahead of time, so that there’s actually nothing to evaluate at all. As long as most of the auxiliary variables spend most of their time in the dark state, the amount of work you have to do at each step can be greatly reduced. Of course, you have a transition rule for the auxiliary variables too. The effect is that these variables blink on and off over time – hence, Firefly Monte Carlo.

NV: There is a number of ways to accelerate MCMC, like hamiltonian, stochastic gradient, etc. What distinguishes your approach? Can you explain it in practical terms? What does this mean for a data scientist?

DM: Yes, there’s been a huge amount of work on accelerating MCMC. Firefly Monte Carlo takes the approach of accelerating MCMC by reducing the cost of likelihood evaluations, specifically by using subsets of data at each step. Compared to most other methods that take the same approach, like Yee Whye Yeh and Max Welling’s stochastic gradient Langevin dynamics, Firefly has the advantage of being exact, in the sense that it targets the true posterior distribution rather than an approximation. The downside is that it’s much less general. One nice thing about Firefly Monte Carlo is that it plays nicely with many other MCMC methods. For example, you can use your favorite transition operator, whether it’s Hamiltonian dynamics or slice sampling, on top of Firefly Monte Carlo.

NV: Do you have any success stories to share? Companies using FlyMCMC in production?

DM: Sorry Nick, got nothing here! (But I haven’t been following it too closely either)

NV: In your paper you present some experiments on a deep model. Your method seems to need very few model evaluations on small sample sizes. It seems like it can compete with SGD. Have you tried training a deeper model with FlyMCMC? Do you think MCMC methods can replace SGD in deep learning? Would that help in better generaliation?

DM: Unfortunately, Firefly Monte Carlo doesn’t work with neural networks beyond “zero hidden layers” models like straight logistic regression and softmax classification. The problem is that it’s hard to come up with a general lower bound on the likelihood for the sorts of complicated likelihoods you get with multi-layer neural networks.

NV: Most of the accelerated MCMC methods do not apply in all problems. What are the limitations of FlyMCMC? Can you mention cases where it cannot be used?

DM: The big limitation is that it only works for likelihoods for which you can construct a collapsible lower bound. The other limitation is that introducing the auxiliary variables can slow down mixing. But it’s very hard to make formal statements about mixing times. In the experiments we ran, we found that mixing speed was slower than for regular MCMC, but it was more than compensated for by the reduced number of likelihood calculations. But these are empirical results for a few particular models and data sets, so we can’t know how widely applicable they’ll be.

NV: Thank you Dugal. If you want to find more about UAI best papers visit our blogpost here: https://www.linkedin.com/pulse/best-paper-awards-uai-conferences-nikolaos-vasiloglou